Cuando hablamos diagramas p-q, intrínsecamente nos estamos refiriendo también a la trayectoria de esfuerzos que se producen en el suelo cuando se aplica una carga. A lo mejor es la primera vez que oyes hablar sobre este concepto, pero estoy seguro de que alguna vez has visto diagramas p-q o has hecho un análisis de trayectoria de esfuerzos. Es un concepto que realmente no es nuevo, pero por alguna razón, no es habitual encontrar profesionales de la geotecnia que los manejen con cierta soltura.
Como siempre, te recomendamos algunas entradas que te van a servir de base:
- Consolidación de suelos. Parámetros de laboratorio.
- Resistencia al corte sin drenaje en arcillas.
- SHANSEP. Método y resistencia al corte.
- Ensayo triaxial.
Este último, el del ensayo triaxial, es el más importante. Un diagrama p-q de cada probeta ensayada es algo que siempre tendremos de este tipo de ensayo.
¿Qué son los diagramas p-q?
Es un artificio gráfico para mostrar los datos obtenidos en un ensayo, normalmente un triaxial, para ilustrar de manera gráfica cómo es el comportamiento del suelo durante un proceso de carga.
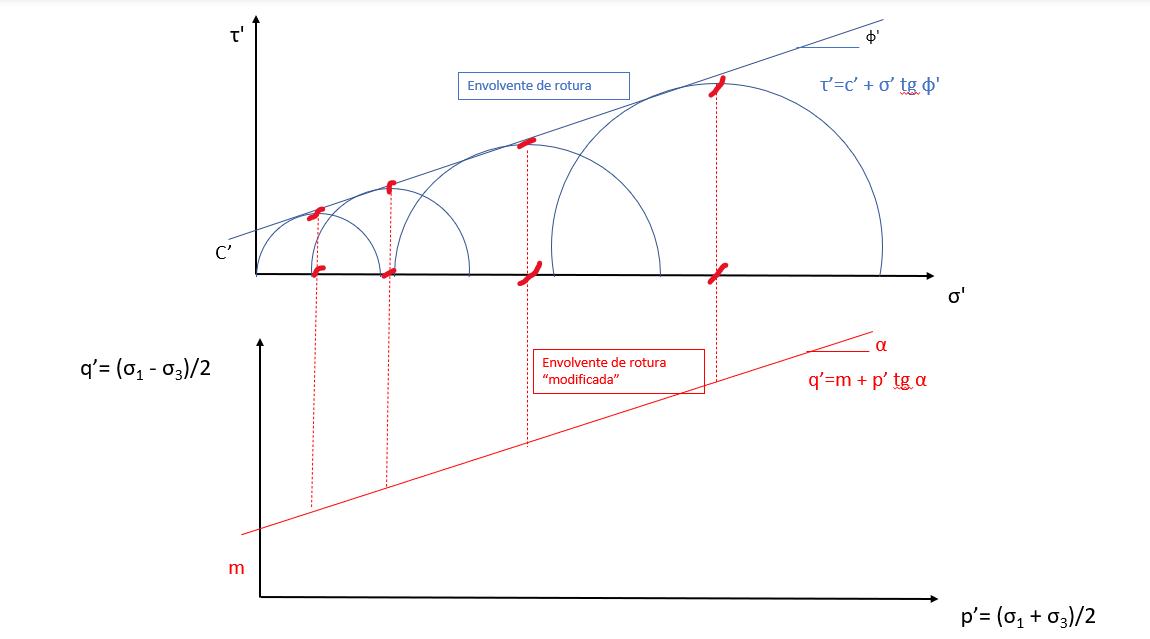
Con el ensayo triaxial obtenemos los famosos círculos de Mohr, pero no resulta útil dibujarlos, sobre todo cuando quieres representar los círculos intermedios (antes de la rotura). Es por eso que se representa sólo los puntos superiores (p’) y el centro de cada círculo (q’).
Lo intentamos ilustrar con esta gráfica.
Si recapitulamos lo visto hasta ahora:
- p’ representa el centro de cada circulo y q’ su radio.
- La envolvente modificada es parecida a la original, pero no es exactamente la misma. La razón es que se construye con las tangentes a los círculos y la modificada con los puntos superiores.
- Para pasar de una envolvente a otra podemos usar estas fórmulas.
¿Por qué son útiles?
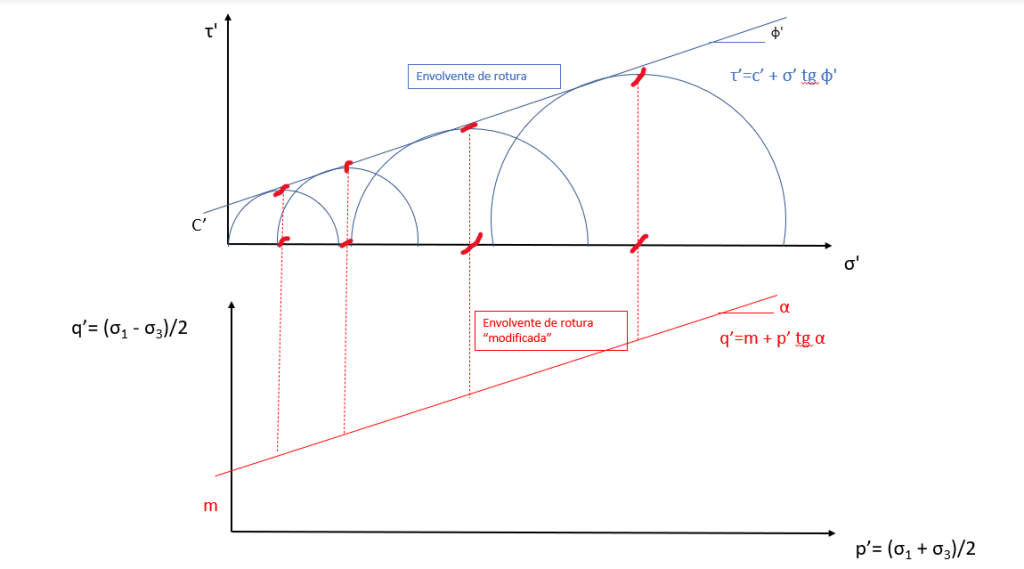
De entrada nos hemos quitado de en medio los círculos de Mohr, pero también podemos mostrar la información valiosa que tienen los círculos antes de la rotura. Esta figura ilustra cómo sería:
La línea roja es la trayectoria de esfuerzos que pasa por los puntos superiores de cada círculo.
Mientras se realiza un ensayo triaxial, los valores de p’ y q’ varían hasta llegar a la rotura.
¿De qué depende? Básicamente de cómo se diseñe el ensayo (por ejemplo, drenado o no drenado) y de la naturaleza del suelo. Hay suelos que ensayados en las mismas condiciones tienen trayectorias de esfuerzos distintas. Si aprendes a leer los diagramas p-q tendrás en tu poder mucha información relevante.
Tipos de diagramas p-q
En las siguientes líneas vamos a ver qué diagramas nos vamos a encontrar y cómo los podemos interpretar. Como decíamos hace un momento, lo primero que habrá que ver es el tipo de condiciones del ensayo, que las podemos reducir a condiciones CD o CU.
Ensayo CD
Si recordamos lo que veíamos en la entrada del ensayo triaxial, sólo podríamos obtener la trayectoria de esfuerzos efectivos (ESP) ya que las presiones de poro son nulas. Además, como existe drenaje durante la aplicación de la carga, la presión de confinamiento efectiva (σ’3) no varía.
Teóricamente la trayectoria de presiones efectivas (ESP) es un línea recta que forma 45° con la horizontal. Esta trayectoria la tendremos tanto en materiales que podemos considerar drenados (arenas) como arcillas que se someten a una carga tan lenta, que se permite la liberación de presiones de poro.
Ensayo CU
Las trayectorias que se dan en estos ensayos son más interesantes, porque según el tipo de suelo, las trayectorias pueden variar. Recordemos que en condiciones no drenadas se generan presiones de poro)
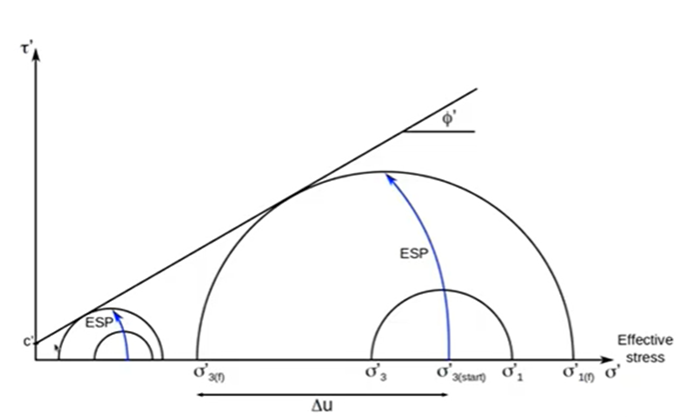
En general, el comportamiento más habitual del suelo en condiciones CU será el que se ilustra en esta figura.
La gran diferencia es que en estas condiciones la presión de confinamiento efectiva (σ’3) va siendo cada vez menor ya que, al aumentar la carga (σ’1) y no permitirse el drenaje, la presión de poro (u) va aumentando. Es curioso, conforme aumentamos la carga, la presión de confinamiento se reduce.
Suelos contractivos y dilatantes
Vamos a hacer un pequeño acercamiento a este concepto, porque la idea es dedicarle una entrada completa. El asunto lo merece.
De alguna manera asumimos que al aumentar la carga (σ’1) siempre va a aumentar la presión de poro, pero esto no es así siempre. Toma nota: las presiones de poro pueden ser negativas y por lo tanto nuestra trayectoria de esfuerzos se desplazaría hacía la derecha. Ya lo veíamos cuando hablábamos del ensayo triaxial. ¿Te acuerdas de esta imagen?
Allí ya veíamos que los suelo podían tener un comportamiento dilatante o contractivo.
La A de Skempton
Para esto nos va a interesar manejar el siguiente parámetro: la A de Skempton.
A= Δu/σ’d
Siendo σd el esfuerzo desviador (σ’1– σ’3)
Este parámetro permite evaluar cómo varían las presiones de poro conforme aumenta la carga, y sirve para clasificar los suelos según su valor:
Contractivos
- A < 0.5
- Δu > 0
- las presiones efectivas disminuyen respecto a las totales
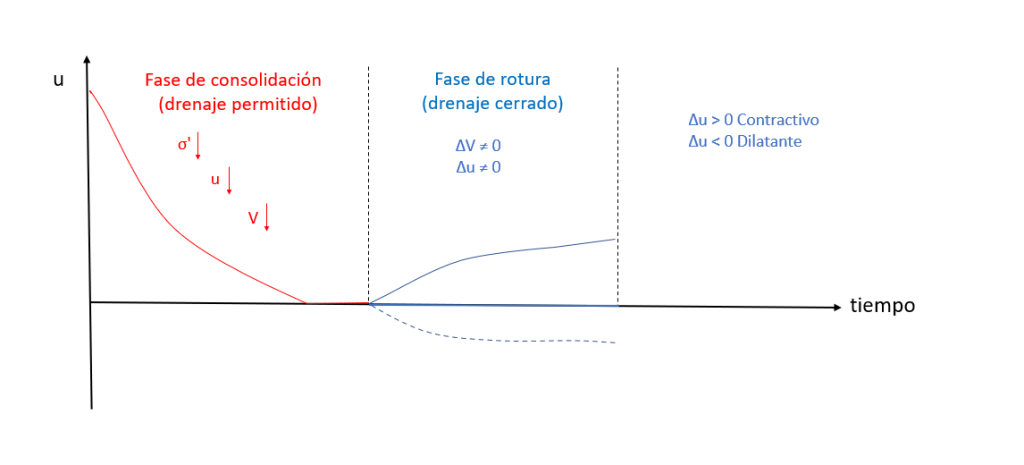
Si pudiéramos modelizar el comportamiento contractivo del terreno durante el ensayo, sería algo así como esto:
Es el comportamiento habitual de las arcillas blandas (no consolidadas) y las arenas sueltas.
Dilatantes
- A > 0.5
- Δu < 0
- las presiones efectivas aumentan respecto a las totales
El mecanismo interno que sufriría un suelo dilatante sería como esta imagen.
Este es el comportamiento típico de arenas densas y en arcillas sobreconsolidadas.
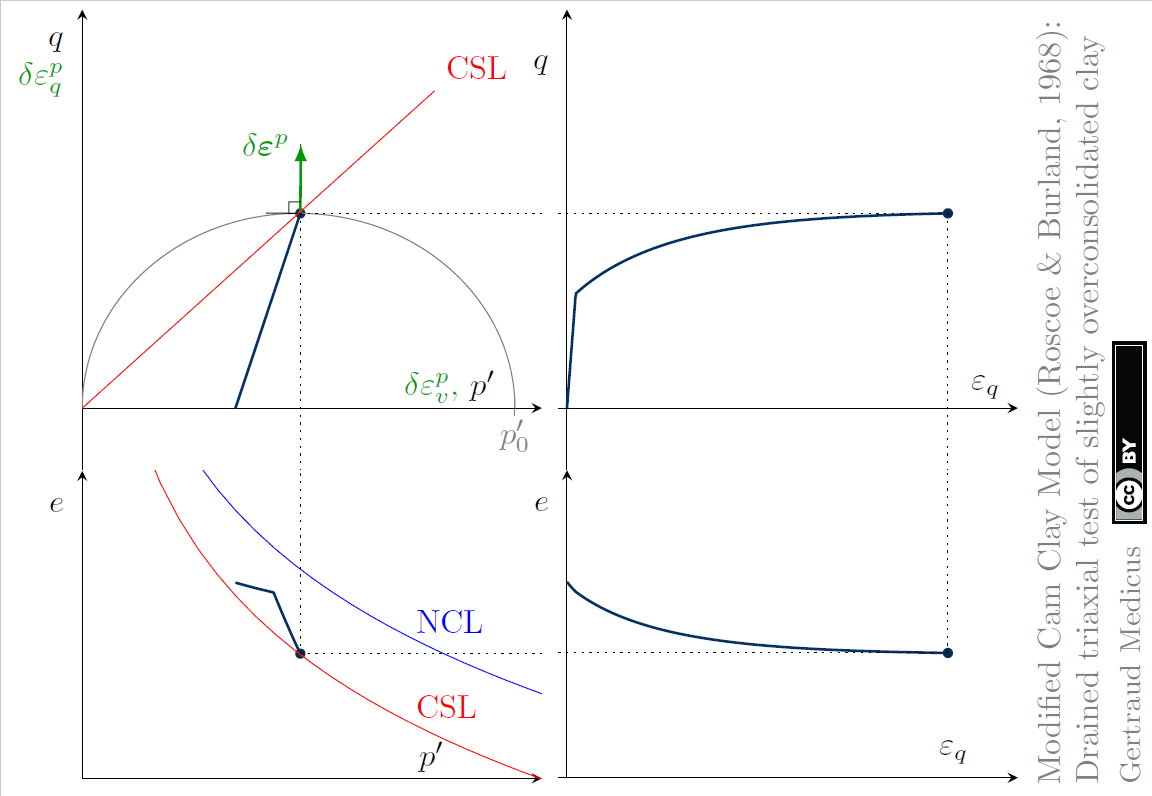
La realidad a veces es más compleja. Esta es la imagen de una trayectoria de esfuerzos de un ensayo triaxial.
Al principio del ensayo se comporta como un suelo dilatante, pero conforme empieza a reajustarse adquiere un comportamiento claramente contractivo. Cuando se produce la rotura aparece un cambio en la estructura del suelo y por un momento, aumenta el valor de p y q (dilatante) y luego se reduce el valor de ambos. Este comportamiento, que se da tras la rotura también será interesante conocerlo.
Conclusiones de diagramas p-q
Decía el profesor Bob Holtz que “en la práctica geotécnica, si tú entiendes la trayectoria de esfuerzos completa, estarás en el camino directo de la solución del problema”.
De verdad, es muy importante manejar este tipo de gráficas, saber en qué condiciones se va a hacer la carga, el rango de esfuerzos de nuestro proyecto, cómo se va a comportar el suelo, etc. A veces nos ponemos a modelizar, a hacer ensayos y proponer soluciones sin realmente pararnos a analizar fríamente el problema. Es muy importante que nuestra estrategia de investigación se ajuste a lo que el proyecto y el terreno necesita.
Seguiremos hablando sobre estos temas porque son muy interesantes. En breve trataremos en el blog sobre el fenómeno de la dilatancia y profundizaremos en la resistencia al corte de suelos arcillosos.
Muchas gracias por vuestro tiempo.