La dilatancia en suelos es un fenómeno que se puede observar (y cuantificar) tanto en suelos granulares como en cohesivos. En principio puede parecer un comportamiento “anormal” del suelo, pero nada más lejos de la realidad.
Creo que tratar este tema en el blog nos va a ayudar a clarificar la resistencia al corte de los suelos, mejorar la interpretación de ciertos gráficos, pero sobre todo empezar a comprender qué tipo de ángulo de rozamiento (también la cohesión pero por otros motivos) es realmente un parámetro intrínseco del suelo. Cómo influye la densidad relativa (“grado de compactación”) y/o su historia tensional. Por último, nos va a permitir hacer una introducción del Modelo del Estado Crítico de los Suelos (CSSM, por sus siglas en inglés).
No es un tema nuevo en el blog. Ya vimos algo de este fenómeno en estos post:
¿Qué es la dilatancia?
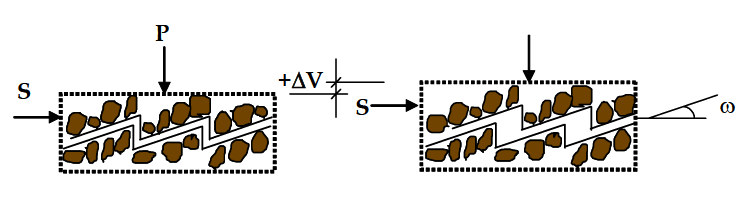
La dilatancia es una variación del volumen cuando se aplican tensiones tangenciales. Se mide en grados y la vais a ver expresada con distintos símbolos (ω, ψ, α) así que no os preocupéis mucho por esto. La siguiente figura ilustra bien el comportamiento.
La interpretación es la siguiente: cuando aplico una fuerza tangencial (S), el bloque superior desliza y tiende a moverse verticalmente, provocando un cambio de volumen positivo (+ΔV). Siendo ω el ángulo de dilatancia. Quiero señalar que la dilatancia puede ser positiva o negativa, aunque a este último comportamiento se le suele denominar “contractivo”.
El caso es que la resistencia al corte vendrá determinada por la siguiente expresión (considerando la cohesión como cero):
S = tan (φ+ω)P
Siempre hemos considerado que sólo existe φ (ángulo de rozamiento interno entre las partículas sólidas del suelo), pero existe otro ángulo (ω). El resultado de un ensayo de corte directo o triaxial es un “ángulo” que incluye tanto φ como ω. Veremos un poco más adelante cómo separar el grano del trigo, o lo que es lo mismo saber separa el φ de ω, ya que φ es el que realmente es constante y ω varía en función de la densidad relativa o la sobreconsolidación, dependiendo si estamos hablando de suelos granulares o cohesivos. Y de esto mismo vamos a hablar a continuación.
Dilatancia en suelos granulares
Fundamentalmente depende de la compacidad o en términos más cuantitativos, de la densidad relativa como ilustra la siguiente figura.
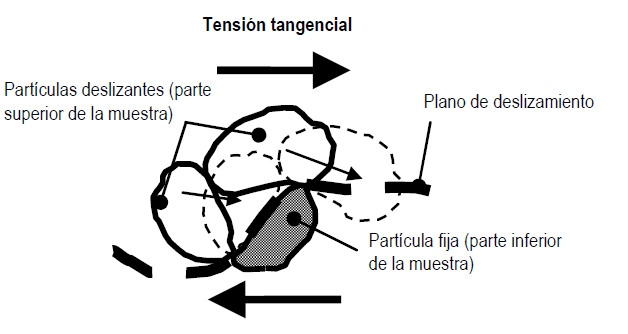
El mecanismo de dilatancia positiva, en suelos densos, se ilustra en la siguiente figura.
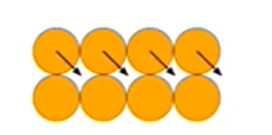
En suelos sueltos, la dilatancia es negativa y el mecanismo es como se representa a continuación.
Dilatancia en suelos finos
En suelos finos no hablamos de densidad relativa. Más bien hablamos en términos de índice de poros.
En este caso, el factor relevante es la sobreconsolidación del suelo (OCR). Un suelo sobreconsolidado, es decir que haya estado sometido a presiones verticales superiores a las que soporta actualmente, y será más “denso” que un suelo normalmente consolidado que lo podemos considerar como “suelto”. Con valores de OCR mayores a 3 se observará claramente la presencia de una resistencia al corte “pico”.
El mecanismo de dilatancia en suelos finos sería tal y como se representan es estas figuras.
- Positiva.
- Negativa (contractivo)
Dilatancia con o sin drenaje
En el caso de suelos cohesivos, la dilatancia la observaremos de distinta manera si el fenómeno ocurre con drenaje (se permite cambio volumétrico) o no está permitido (no se permite).
Drenado.
El fenómeno es parecido al caso de suelos granulares, aunque en la magnitud es considerablemente menor.
No drenado.
En los ensayos en los que la variación volumétrica no está permitida, la dilatancia se expresará a partir de la medición de la presión de poro. ¿Os acordáis de esta figura? Seguro que sí, no es la primera vez que la usamos.
Ya decíamos en su momento que:
- Contractivos o dilatante negativo (Δu>1): Tienden a consolidar. Se da en suelos sueltos y arcillas normalmente consolidadas (NC).
- Dilatante o dilatante positivo (Δu<1): Tienden a dilatar (expandirse). Se da en suelos densos y arcillas sobreconsolidadas (OC).
Como veis, vamos dando vueltas un poco a lo mismos conceptos pero cada vez, sacamos más información.
Cuando veíamos los diagramas p-q hablábamos de la A de Skempton (A= Δu/σ’d), siendo σd el esfuerzo desviador (σ’1– σ’3). Este parámetro permite evaluar cómo varían las presiones de poro conforme aumenta la carga, y sirve para clasificar los suelos según su valor.
- A < 0.5: Contractivo
- A > 0.5: Dilatante
Diagrama esfuerzo-desplazamiento-índice de poros
Ya sabemos que tanto los suelos granulares como los cohesivos, cada uno por sus razones, podemos considerar que la dilatancia positiva (o simplemente dilatantes) está asociada a suelos “densos” mientras que los suelos la negativa (contractivos) lo está a suelos “sueltos”. Si representamos estás dos situaciones veremos que los dilatantes presentan una resistencia pico que la que genera la existencia de la dilatancia. Es decir hay un trabajo (en términos energéticos) adicional que vencer para producir la falla del suelo.
La gráfica habla por sí misma pero la describimos brevemente:
- Suelto: Parte de una relación de vacíos (e) alta y cae hasta ecrítica. La pendiente de la curva es más o menos constante. De igual manera, de manera progresiva va ganando resistencia al corte hasta llegar τu . Digamos que su comportamiento es más homogéneo.
- Denso: Parte de una relación de vacíos (e) baja y al dilatar, aumenta “e” hasta alcanzar ecrítica, pero no lo hace de manera progresiva. De hecho la curva en la gráfica de e-δ coincide, como es lógico, con el pico de resistencia. Luego la resistencia desciende hasta τu
Lo interesante es que, independientemente de las condiciones iniciales del suelo, la resistencia última de un suelo y el valor mínimo de índice de poros (ya no hay cambio de volumen), es única. Realmente estos dos valores son los que podemos considerar intrínsecos a un suelo.
Interpretación de Ensayo de Corte Directo.
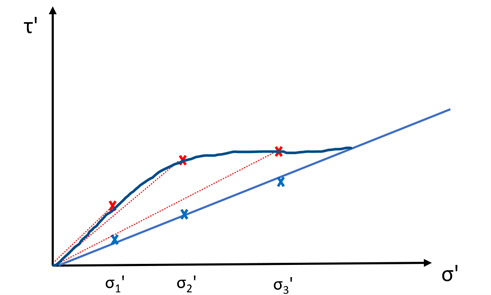
Este ensayo es el que intuitivamente nos ayuda mejor a entender el fenómeno de la dilatancia, ya que aplicamos el esfuerzo sobre un plano horizontal definido. Para interpretar correctamente el ensayo, para cada muestra que tomemos debemos calcular tanto la resistencia “pico” (en rojo) como la “ultima” (en azul).
Si ensayamos varias muestras de un mismo suelo a diferentes presiones de confinamiento, veremos que la resistencia última o residual es siempre la misma. Es el verdadero ángulo de rozamiento intrínseco del suelo. Para cada una de las probetas también tendremos un valor de resistencia pico que dependerá del valor de la dilatancia. La verdadera gráfica es curva al principio y cuando las presiones de confinamiento son altas (bajo valor de índice de poros), la resistencia de la muestra es la residual.
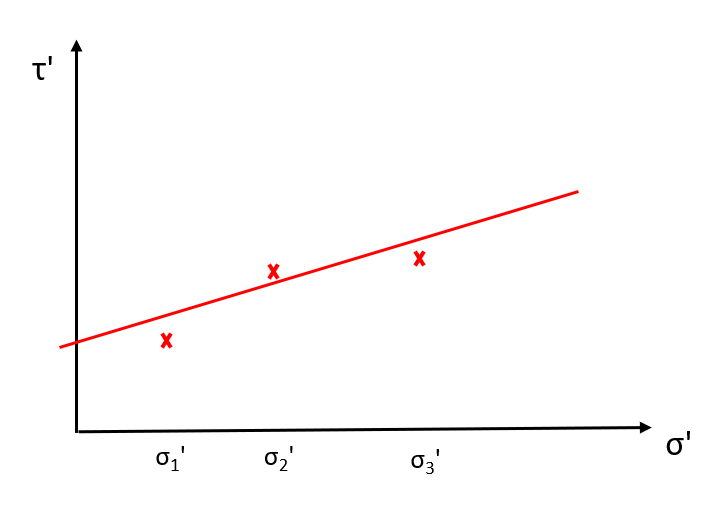
Es muy importante conocer este fenómeno porque podemos tener la tentación de sólo considerar la resistencias pico (los puntos rojos) y hacer esto:
Pues sí, esto es conceptualmente incorrecto. Estaríamos dando unas propiedades resistentes al suelo que no tiene. Dicho de otro modo, hay combinación de σ‘ y τ en los que según está gráfica no fallaría y esto no es así.
Conclusión sobre la dilatancia
La verdad es que espero que se haya comprendido el fenómeno. No es sencillo, esa es la verdad, pero debemos fijarnos que siempre nos movemos en los mismos conceptos: presión de confinamientos y de poro, volumen, índice de poros, resistencia al corte, …y poco más. Es muy importante que siempre que interpretéis ensayos de resistencia.
Por último nos ha servido para afianzar conceptos que nos van a venir muy bien cuando revisemos Modelo del Estado Crítico de los Suelos (CSSM). Os adelanto que lo que hemos visto sobre la resistencia e índice de poros últimos será muy importante manejarlo bien.
Muchas gracias por vuestro tiempo y como siempre, animaos a comentar.
