Inclinómetros. Cálculo y representación de deformaciones del terreno.

De nuevo Abrahan González Sánchez colabora en el blog aportando su amplio conocimiento sobre los distintos aspectos de los inclinómetros. En esta entrada nos cuenta cómo calcular y representar las deformaciones del terreno a partir de medidas de los inclinómetros.

¡Gracias de nuevo, Abrahán!

Hace tiempo que dedicamos un artículo a explicar los aspectos teóricos de qué son los inclinómetros y para qué sirve (pincha aquí) y otro para hablar sobre cómo se realiza su instalación profesional en obra (pincha aquí). Finalizamos esta serie de artículos compartiendo los detalles de cómo calcular y representar las deformaciones del terreno a partir de los datos de medida del inclinómetro.

Queremos señalar que algún fabricante puede introducir alguna variable que aquí no citemos, aunque lo normal es que podáis trabajar con la información que os suministramos a continuación.

¿Qué miden los inclinómetros?

Antes de entrar en harina, hagamos un breve recuerdo de qué mide los inclinómetros de manera que sea más comprensible el proceso de toma de datos, cálculo e interpretación de resultados.  En un punto cualquiera de medida, con el inclinómetro se obtiene la distancia horizontal que hay entre la posición real de la tubería inclinométrica en dicho punto y una línea vertical teórica que pase por él. Al obtener medidas sucesivas en el tiempo sobre el mismo punto, puede apreciarse su deriva espacial y calcular, entre otras cosas, su velocidad de desplazamiento.

Conceptos básicos de medida

La frase “tan técnica” con la que definimos qué miden los inclinómetros requiere aclaración y encierra los conceptos básicos de medida con este instrumento geotécnico. Comencemos a desgranarla:

1. Recordemos que la distancia horizontal será medida tanto en el EJE A como en el EJE B. Los inclinómetros son BIAXIALES por lo que la lectura en ambos ejes se toma de manera simultánea. No es necesario medir en A y luego en B, una única “pasada” sobre el inclinómetro permite obtener la posición en ambos ejes.

2. Cuando hablamos de “un punto cualquiera de medida” no queremos decir que midamos una única vez en la tubería inclinométrica. En cada tubería se realizan medidas a lo largo de su fuste, habitualmente con una separación de 0.5 m. Esta separación es conocida en el argot como PASO DEL INCLINÓMETRO o simplemente PASO. Es decir, sobre una tubería de 10 m de fuste se efectuarán 20 lecturas del EJE A y otras 20 lecturas del EJE B cada 0.5 m de separación. La curva que une estos 20 puntos dibujará la posición real de la tubería en el espacio proyectada en el EJE A y en el EJE B, es decir, sus componentes XY.

3. La toma sucesiva en el tiempo de las posiciones XY en una misma tubería inclinométrica, cada 0.5 m (o el PASO que se desee), reflejará los desplazamientos horizontales que se producen en ella a lo largo de su fuste y permite tomar acciones preventivas en obra.

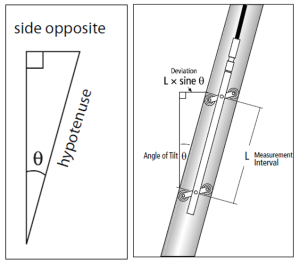
4. Debemos pensar que en cada punto donde efectuemos una lectura, tanto para el EJE A como para el EJE B, nuestro problema se reduce a saber cuánto miden los tres lados de un triángulo rectángulo. En dicho triángulo, la longitud L del inclinómetro (el torpedo en sí, pincha aquí) constituye la hipotenusa y su magnitud es igual a la distancia de fabricación entre ejes, normalmente 0.5 m (igual que el PASO).

El CATETO MENOR del triángulo determina la posición real de la tubería inclinométrica, es el dato que perseguimos. La posición teórica vertical de la tubería, equivale al CATETO MAYOR del triángulo, que no nos interesa. En esquema es así:

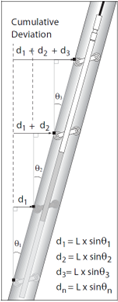
5. Podemos afirmar que el inclinómetro mide el ángulo θ que forma la tubería inclinométrica respecto de la vertical. Sus componentes XY son el SENO TRIGONOMÉTRICO de dicho triángulo en los EJES A y B respectivamente. Como realizamos una lectura de la posición de la tubería cada 0.5 m, la suma acumulativa de los SENOS o CATETOS MENORES obtenidos en cada medida nos ofrece la posición real XY de la tubería inclinométrica en el espacio a lo largo de su fuste.

d_n = Cateto menor.    

θ_n = Ángulo respecto de la vertical en cada punto de medida.

6. Es práctica habitual que los fabricantes de instrumentos de medida añadan una CONSTANTE INSTRUMENTAL que, aplicada sobre el ángulo medido por el instrumento, permita obtener directamente el valor o tamaño del CATETO MENOR y en las unidades deseadas. Habitualmente el aparato se diseña de modo que la CONSTANTE INSTRUMENTAL sea igual a L de manera que el cálculo se simplifique, lo veremos más adelante.

7. Aunque para obtener la posición de la tubería no es estrictamente necesario, para minimizar errores en el proceso de toma de datos y mejorar la calidad de la lectura, los softwares de medición (y en la práctica profesional es también recomendable) están diseñados de manera que la posición de la tubería en un punto sea obtenida a partir de la media aritmética de dos valores que podemos llamar d₀ y d₁₈₀ (el primer y el segundo valor medidos sobre un mismo punto, tendremos que realizar dos “pasadas” o medidas en un mismo punto).

Como los datos se toman para el EJE A y para el EJE B, nuestras magnitudes medidas se denominan en realidad en el argot geotécnico como:

• A0 y A180 para las medidas sobre al EJE A (EJE X).
• B0 y B180 para las medidas sobre al EJE B (EJE Y).

Con todo lo dicho, la ecuación fundamental que permite obtener el desplazamiento d, la posición XY (EJE A y EJE B respectivamente) de un punto de una tubería inclinométrica, a una profundidad de medida n, y el convenio de signos aplicado en el sector, son:

• Si el movimiento en el EJE A es hacia A0, d_A tendrá sigo positivo.
• Si el movimiento en el EJE A es hacia A180, d_A tendrá sigo negativo.
• Si el movimiento en el EJE B es hacia B0, d_B tendrá sigo positivo.
• Si el movimiento en el EJE B es hacia B180, d_B tendrá sigo negativo.

Representación de datos de las medidas de inclinómetros

Pero, queda una pregunta importante aún por resolver.

¿Cómo representamos los datos a partir de los valores d_n obtenidos en cada inclinómetro de modo que sean interpretables?

El proceso es laborioso y según las habilidades de cada cual con bases de datos y hojas de cálculo puede ser más o menos complicado. Los fabricantes ofrecen softwares de interpretación y representación con salidas gráficas y corrección de errores que facilitan mucho el trabajo a cambio de un coste económico. No obstante, pueden programarse las operaciones fácilmente en una hoja de cálculo. A continuación, describimos el proceso y finalmente incluiremos unos gráficos de presentación de resultados a modo de ejemplo:

1. Lo primero que tenemos que saber es que los datos de deformación se representan de manera relativa. Es decir, la primera lectura que se realiza sobre un inclinómetro instalado (en argot, la Lectura Inicial d_i) se considera, por convenio, perfectamente vertical, por lo que todas las deformaciones d_n de ambos ejes y a todas las profundidades serán representadas con el valor X = 0 e Y = 0. Esto se consigue restándole a la primera lectura realizada sobre el inclinómetro los valores d de ella misma. Las siguientes lecturas que se realicen también serán relativizadas a la lectura inicial d_i. Es decir:

d_{i calculada} = d_{i medida} – d_{i medida} → Estos valores serán todos cero.

d_{n calculada} = d_{n medida} – d_{i medida} → Estos valores están relativizados a d_{i medida}

Este hecho parece un capricho pero en realidad ninguna instalación queda perfectamente vertical por muy nueva que esté la máquina de sondeos o por muchos centradores que se usen en la colocación de la tubería. Por tanto y para apreciar la evolución de las deformaciones (sus incrementos), es mejor que todos los puntos de control empiecen con el mismo valor d y se elige el valor d_i = 0. Así por ejemplo, un incremento de deformación de 3.6 mm será visualmente apreciable del mismo modo en todos los datos representados y se evita una posible aberración visual gráfica.

2. A continuación, fijamos en la hoja de cálculo las variables de la ecuación fundamental de cálculo de deformaciones. En el manual de instrucciones de nuestro inclinómetro podremos encontrarlas descritas.

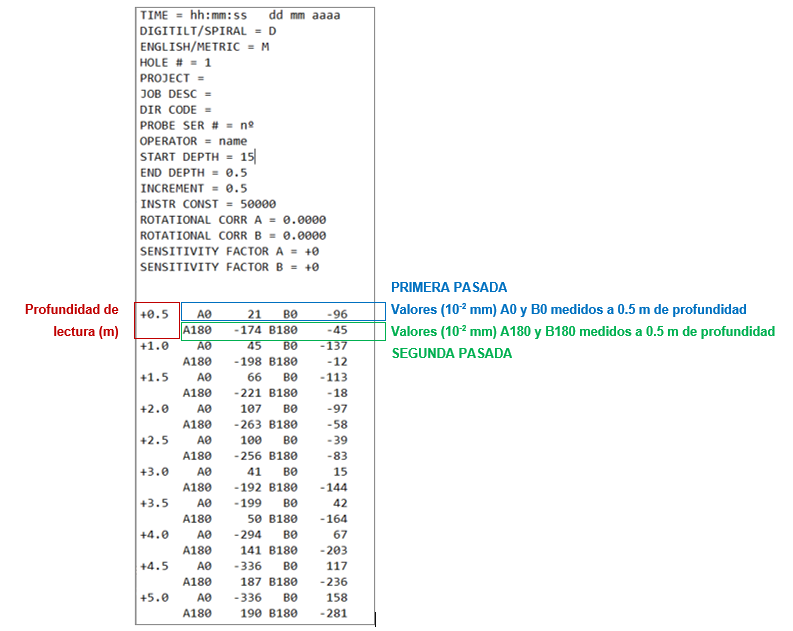
3. Después debemos familiarizarnos con el archivo de datos que genera el software de lectura del inclinómetro. El software de lectura es absolutamente necesario y es independiente del software de interpretación y representación mencionado anteriormente. Estos archivos suelen ser tipo txt y pueden importarse a cualquier hoja de cálculo. En la cabecera están los datos relativos al proyecto y al equipo de lectura, incluida la CONSTANTE y el PASO. Debajo, ordenados en filas están los datos de las medidas d en los diferentes ejes a cada profundidad de lectura.

4. Ya con los datos de una medida importados en la hoja de cálculo, debe obtenerse el desplazamiento d_n para cada EJE y en cada profundidad aplicando la ecuación fundamental. Posteriormente serán relativizados a la lectura inicial. A continuación, deberán ser sumados de manera acumulativa para obtener la posición relativa de la tubería a lo largo de todo su fuste.

Los valores d_{n calculados} para cada EJE serán cero en la zona donde el inclinómetro no sufra deformaciones. Típicamente en la base de la tubería que debe alcanzar terreno firme estable, y presentarán incrementos en las zonas con desplazamiento.

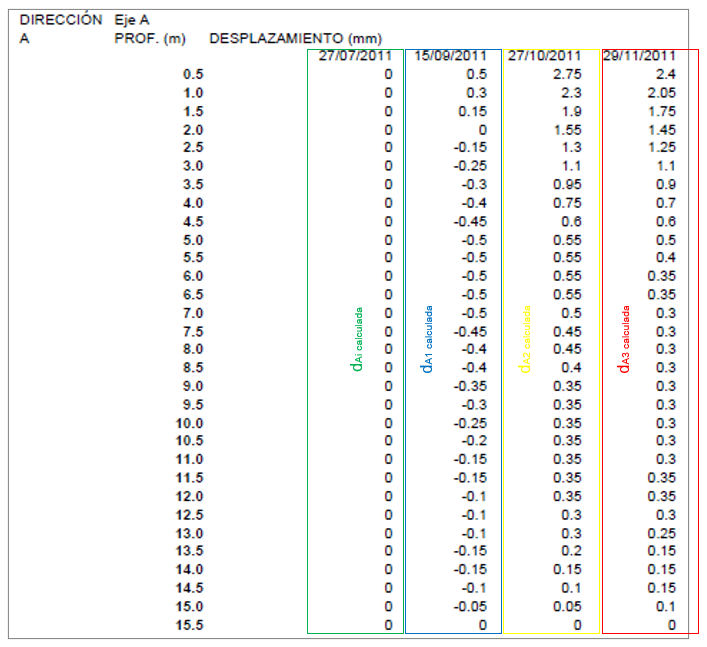
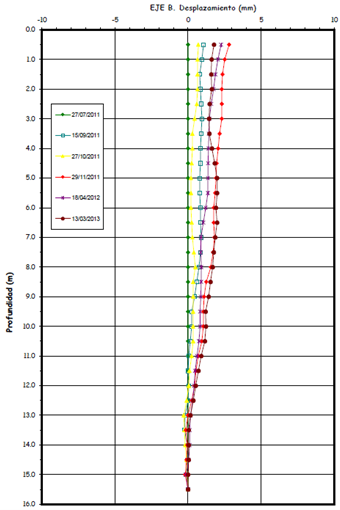
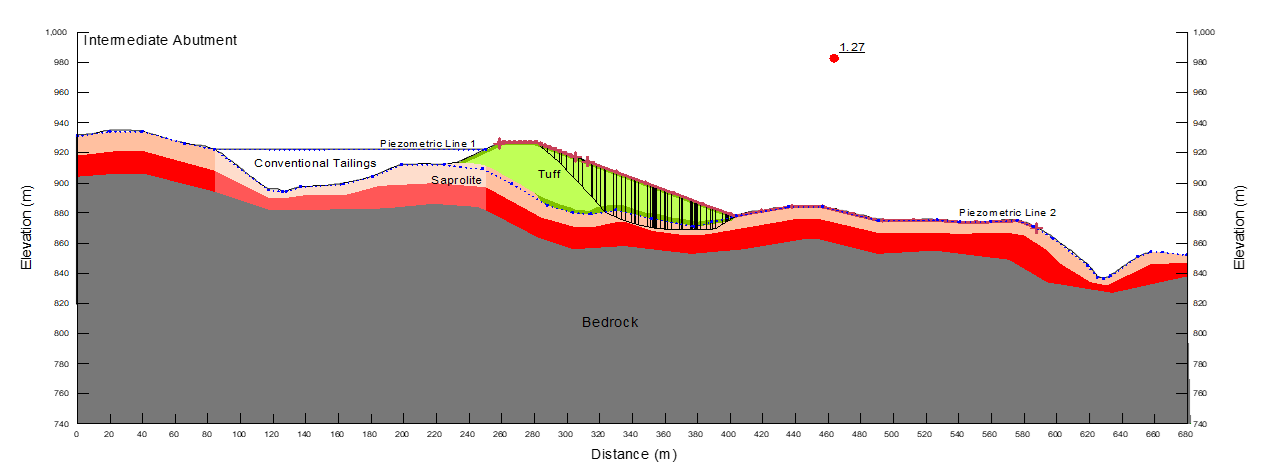
5. Calculados y ordenados todos los valores d_n, es hora de efectuar una representación gráfica. Esto va a permitir abordar el estudio de la evolución de las deformaciones. A continuación, os dejamos unos ejemplos básicos pudiéndose incluir más informaciones del proyecto como: cotas, niveles semafóricos de aviso/intervención, velocidades de deformación, etc.

Esperamos que este artículo que culmina la serie sobre inclinómetros os permita un mejor desempeño de la profesión de geólogo-geotécnico.

Salu2!