Hablando hoy de la cantidad económica de pedido es una manera de cumplir con uno de los objetivos de este blog. Vamos a tratar de colaborar en la medida que se pueda a mejorar las tareas que los profesionales de la construcción, y más concretamente, de las especialidades del mundo de las cimentaciones especiales y tratamientos del terreno.
Dentro de las actividades, fuera aparte de los aspectos técnicos que son muchos y muy importantes, encontramos las tareas de gestión. Hoy veremos cómo podemos mejorar nuestros procesos de logística y adquisición de materias primas.
¿Qué es la cantidad económica de pedido?
En el día de hoy vamos a presentar, de manera muy sucinta, un método de trabajo que nos permita conocer cuál debe ser la “cantidad” (y frecuencia) de pedido a realizar de un material consumible en obra (piezas, repuestos, materiales incorporables, etc.) de tal manera que optimicemos costes.
Por centrar un poco el tiro, vamos a imaginar que nuestra obra consiste en realizar unas inyecciones de lechada de cemento para realizar una pantalla de impermeabilización en una presa. Alguno pensará: ¿seguro que hace falta calentarse tanto la cabeza para saber cuánto cemento hay que pedir en cada pedido y las veces hay que hacer el mismo? La cuestión empieza a tener especial relevancia si nos imaginamos que la obra ya nos es que no esté cerca de un punto habitado, sino que está en lugares inaccesibles como puede ser la selva tropical de África.
Pues bien, apoyándonos en este ejemplo que es perfectamente real, vamos a hacer un desarrollo de este modelo al que luego le podremos cifras para que la explicación sea más efectiva.
Principios teóricos “Cantidad económica de pedido” (Q)
Como decíamos es un modelo fundamental de control de inventarios, y se basa en encontrar el punto en el que los costos por pedir un producto y los costos por mantenerlo en inventario son iguales.
Los principios fundamentales de la cantidad económica de pedido son:
-
La demanda es conocida, constante e independiente.
Debemos suponer que este dato lo tenemos que conocer con cierta certidumbre, sino mal vamos…
-
El tiempo de reabastecimiento del proveedor es constante y conocido.
Tampoco es difícil suponer que es así.
-
El inventario se reabastece instantáneamente cuando llega a cero, con la llegada del lote pedido.
Bueno, esto viene a decir que el pedido llega justo cuando se vacía el silo (o los silos) de cemento. Esto no va a ser así, pero vamos a mantener el supuesto, sabiendo que desarrollos más complejos del modelo contempla que mantenemos una cantidad mínima de stock.
-
No existen descuentos por volumen de pedido.
Esto frecuentemente no es así, pero por motivos didácticos mantendremos este supuesto también.
-
Los costes totales son la suma de:
– Costes de Compra. Es un coste variable: costo unitario de compra (C) × demanda del periodo (D). Normalmente nos pedirán un pedido mínimo, pero esto no lo vamos a tener en cuenta.
– Costo de pedido. Cada pedido tienen un costo fijo S y se pide D/Q veces por año. Corresponde a S × D/Q.
– Costo de mantener inventario (de almacenamiento). Si la cantidad de inventario promedio es Q/2, el costo será H × Q/2.
Por lo tanto, el coste total (TC) será:
La gráfica de esta ecuación tendría la siguiente forma.
Minimiza los costes
El valor de Q que optimice los costes totales no es otro que aquel que minimice la ecuación. Para ello, y cómo podemos recordar de nuestra época del bachiller, hay que derivar la ecuación respecto a Q e igualar a cero.
Si despejamos Q, llegamos a una ecuación que nos permite conocer hallar su valor óptimo:
Como vemos:
- No depende del coste unitario del material (C). En otras palabras del precio.
- A mayor demanda (D) y mayor coste fijo por cada pedido (S), mayor tamaño del pedido.
- A mayor coste de mantener inventario (H), de menor tamaño será cada pedido.
La frecuencia de pedido (veces durante el periodo considerado) va en sentido contrario a lo anteriormente comentado:
Aplicación práctica
Y como lo prometido es deuda, vamos a poner cifras lo más “reales” posibles al ejemplo que citábamos un poco más arriba. Imaginaremos que la obra dura 24 meses, y que conocemos trabajamos con los siguientes datos:
C = 300 €/Tn. Incluye transportes e impuestos proporcionales.
S = 2000 €/pedido. Lo que nos cobra una empresa externa por gestionar, nacionalizar el material, tasas fijas, etc. Es un gasto fijo en cada pedido.
D= 70 Tn/mes.
H= Esto merece una explicación. El coste mensual contemplará la parte proporcional mensual de:
- Transporte (traerlos y llevárnoslos): 6000 €/silo.
- Acondicionar la zona: 1000 €/silo.
- Alquiler: 300 €/silo al mes.
H= [(6000+1000)/24] + 300 (por mes y por silo)
Finalmente, “H” es la única variable con la que podemos jugar por lo que resulta bastante ilustrativo ver cómo varía la cantidad óptima, la frecuencia y los costes totales en función del coste de almacenamiento.
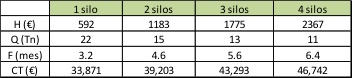
Conclusión
A la luz de los resultados, y sabiendo que la capacidad de un silo convencional es de 25-30Tn de cemento, parece que con un silo y recibiendo 3 pedidos al mes optimizaríamos costes. Sobre el papel esto es así, pero todos convendremos que es una opción un tanto arriesgada, y que lo razonable, con el fin de no tener rupturas de stock, es tener dos silos en obra. No minimizaríamos costes, pero sí podemos optimizarlos haciendo pedidos de 15 toneladas cada 4.5 veces al mes (de media en los 24 meses).
Como os decía, esto es un ejercicio teórico y tiene muchas inconsistencias, como por ejemplo, que el proveedor te permita pedidos tan pequeños (15Tn) y tan frecuentes; y otros muchos como que se le puede ocurrir al lector. El mayor valor de conocer este método que abre la puerta a otros sistemas de gestión de inventarios más complejos y que contemplan pedidos mínimos, mantenimiento de un mínimo de stock, descuentos por grandes pedidos, etc.
Espero que os haya resultado interesante, y si es así, no dudéis en compartir.
¡Os espero pronto de nuevo por aquí!
Muchas gracias.
